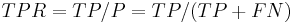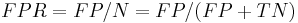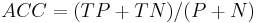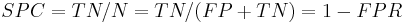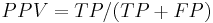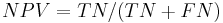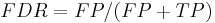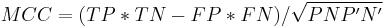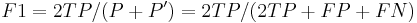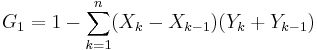Receiver operating characteristic

In signal detection theory, a receiver operating characteristic (ROC), or simply ROC curve, is a graphical plot of the sensitivity, or true positive rate, vs. false positive rate (1 − specificity or 1 − true negative rate), for a binary classifier system as its discrimination threshold is varied. The ROC can also be represented equivalently by plotting the fraction of true positives out of the positives (TPR = true positive rate) vs. the fraction of false positives out of the negatives (FPR = false positive rate). Also known as a Relative Operating Characteristic curve, because it is a comparison of two operating characteristics (TPR & FPR) as the criterion changes.[1]

ROC analysis provides tools to select possibly optimal models and to discard suboptimal ones independently from (and prior to specifying) the cost context or the class distribution. ROC analysis is related in a direct and natural way to cost/benefit analysis of diagnostic decision making. The ROC curve was first developed by electrical engineers and radar engineers during World War II for detecting enemy objects in battle fields, also known as the signal detection theory, and was soon introduced in psychology to account for perceptual detection of stimuli. ROC analysis since then has been used in medicine, radiology, biometrics, and other areas for many decades, and is increasingly used in machine learning and data mining research.

Contents

Basic concept

Terminology and derivations
from a confusion matrix
true positive (TP)
eqv. with hit
true negative (TN)
eqv. with correct rejection
false positive (FP)
eqv. with false alarm, Type I error
false negative (FN)
eqv. with miss, Type II error
sensitivity or true positive rate (TPR)
eqv. with hit rate, recall
TPR = TP / P = TP / (TP%2BFN)
false positive rate (FPR)
eqv. with fall-out
FPR = FP / N = FP / (FP %2B TN)
accuracy (ACC)
ACC = (TP %2B TN) / (P %2B N)
specificity (SPC) or True Negative Rate
SPC = TN / N = TN / (FP %2B TN) = 1 - FPR
positive predictive value (PPV)
eqv. with precision
PPV = TP / (TP %2B FP)
negative predictive value (NPV)
NPV = TN / (TN %2B FN)
false discovery rate (FDR)
FDR = FP / (FP %2B TP)
Matthews correlation coefficient (MCC)
MCC = (TP*TN - FP*FN) / \sqrt{P N P' N'}
F1 score
F1 = 2 TP / (P%2BP') = 2 TP / (2 TP %2B FP %2B FN)

Source: Fawcett (2006).
See also: Type I and type II errors

A classification model (classifier or diagnosis) is a mapping of instances into a certain class/group. The classifier or diagnosis result can be in a real value (continuous output) in which the classifier boundary between classes must be determined by a threshold value, for instance to determine whether a person has hypertension based on blood pressure measure, or it can be in a discrete class label indicating one of the classes.

Let us consider a two-class prediction problem (binary classification), in which the outcomes are labeled either as positive (p) or negative (n) class. There are four possible outcomes from a binary classifier. If the outcome from a prediction is p and the actual value is also p, then it is called a true positive (TP); however if the actual value is n then it is said to be a false positive (FP). Conversely, a true negative (TN) has occurred when both the prediction outcome and the actual value are n, and false negative (FN) is when the prediction outcome is n while the actual value is p.

To get an appropriate example in a real-world problem, consider a diagnostic test that seeks to determine whether a person has a certain disease. A false positive in this case occurs when the person tests positive, but actually does not have the disease. A false negative, on the other hand, occurs when the person tests negative, suggesting they are healthy, when they actually do have the disease.

Let us define an experiment from P positive instances and N negative instances. The four outcomes can be formulated in a 2×2 contingency table or confusion matrix, as follows:

  actual value
  p n total
prediction
outcome		 p' True
Positive		 False
Positive		 P'
n' False
Negative		 True
Negative		 N'
total P N

ROC space

The contingency table can derive several evaluation "metrics" (see infobox). To draw an ROC curve, only the true positive rate (TPR) and false positive rate (FPR) are needed. TPR determines a classifier or a diagnostic test performance on classifying positive instances correctly among all positive samples available during the test. FPR, on the other hand, defines how many incorrect positive results occur among all negative samples available during the test.

A ROC space is defined by FPR and TPR as x and y axes respectively, which depicts relative trade-offs between true positive (benefits) and false positive (costs). Since TPR is equivalent with sensitivity and FPR is equal to 1 − specificity, the ROC graph is sometimes called the sensitivity vs (1 − specificity) plot. Each prediction result or one instance of a confusion matrix represents one point in the ROC space.

The best possible prediction method would yield a point in the upper left corner or coordinate (0,1) of the ROC space, representing 100% sensitivity (no false negatives) and 100% specificity (no false positives). The (0,1) point is also called a perfect classification. A completely random guess would give a point along a diagonal line (the so-called line of no-discrimination) from the left bottom to the top right corners. An intuitive example of random guessing is a decision by flipping coins (head or tail).

The diagonal divides the ROC space. Points above the diagonal represent good classification results, points below the line poor results. Note that the output of a poor predictor could simply be inverted to obtain points above the line.

Let us look into four prediction results from 100 positive and 100 negative instances:

A B C C'
TP=63 FP=28 91
FN=37 TN=72 109
100 100 200
TP=77 FP=77 154
FN=23 TN=23 46
100 100 200
TP=24 FP=88 112
FN=76 TN=12 88
100 100 200
TP=76 FP=12 88
FN=24 TN=88 112
100 100 200
TPR = 0.63 TPR = 0.77 TPR = 0.24 TPR = 0.76
FPR = 0.28 FPR = 0.77 FPR = 0.88 FPR = 0.12
ACC = 0.68 ACC = 0.50 ACC = 0.18 ACC = 0.82

Plots of the four results above in the ROC space are given in the figure. The result of method A clearly shows the best predictive power among A, B, and C. The result of B lies on the random guess line (the diagonal line), and it can be seen in the table that the accuracy of B is 50%. However, when C is mirrored across the center point (0.5,0.5), the resulting method C' is even better than A. This mirrored method simply reverses the predictions of whatever method or test produced the C contingency table. Although the original C method has negative predictive power, simply reversing its decisions leads to a new predictive method C' which has positive predictive power. When the C method predicts p or n, the C' method would predict n or p, respectively. In this manner, the C' test would perform the best. The closer a result from a contingency table is to the upper left corner, the better it predicts, but the distance from the random guess line in either direction is the best indicator of how much predictive power a method has. If the result is below the line (i.e. the method is worse than a random guess), all of the method's predictions must be reversed in order to utilize its power, thereby moving the result above the random guess line.

Curves in ROC space

Oftentimes, objects are classified based on a continuous random variable. For example, imagine that the protein level in diseased people and healthy people are normally distributed with means of 2 g/dL and 1 g/dL respectively. A medical test might measure the level of a certain protein in a blood sample and classify any number above a certain threshold as indicating disease. The experimenter can adjust the threshold (black vertical line in figure), which will in turn change the false positive rate. Increasing the threshold would result in fewer false positives, corresponding to a leftward movement on the curve. The actual shape of the curve is determined by how much overlap the two distributions have.

Further interpretations

Sometimes, the ROC is used to generate a summary statistic. Common versions are:

However, any attempt to summarize the ROC curve into a single number loses information about the pattern of tradeoffs of the particular discriminator algorithm.

Detection Error Tradeoff graph

An alternative to the ROC curve is the Detection Error Tradeoff (DET) graph, which plots the False Negative Rate (missed detections) vs. the False Positive Rate (false alarms), often on logarithmic scales.

Z-transformation

If a z-transformation is applied to the ROC curve, the curve will be transformed into a straight line. This z-transformation is based on a normal distribution with a mean of zero and a standard deviation of one. In strength theory, one must assume that the zROC is not only linear, but has a slope of 1.0. The normal distributions of target and lures is the factor causing the zROC to be linear.

The linearity of the zROC curve depends on the standard deviations of the target and lure strength distributions. If the standard deviations are equal, the slope will be 1.0. If the standard deviation of the target strength distribution is larger than the standard deviation of the lure strength distribution, then the slope will be smaller than 1.0. In most studies, it has been found that the zROC curve slopes constantly fall below 1, usually between 0.5 and 0.9.[3] Many experiments yielded a zROC slope of 0.8. A slope of 0.8 implies that the variability of the target strength distribution is 25% larger than the variability of the lure strength distribution.[4]

Another variable used is d'. d' is a measure of sensitivity for yes-no recognition that can easily be expressed in terms of z-values. d' measures sensitivity, in that it measures the degree of overlap between target and lure distributions. It is calculated as the mean of the target distribution minus the mean of the lure distribution, expressed in standard deviation units. For a given hit rate and false alarm rate, d' can be calculated with the following equation: d'=z(hit rate)- z(false alarm rate). Although d' is a commonly used parameter, it must be recognized that it is only relevant when strictly adhering to the very strong assumptions of strength theory made above.[5]

The z-transformation of an ROC curve is always linear, as assumed, except in special situations. The Yonelinas Familiarity-Recollection model is a two-dimensional account of recognition memory. Instead of the subject simply answering yes or no to a specific input, the subject gives the input a feeling of familiarity, which operates like the original ROC curve. What changes, though, is a parameter for Recollection (R). Recollection is assumed to be all-or-none, and it trumps familiarity. If there were no recollection component, zROC would have a predicted slope of 1. However, when adding the recollection component, the zROC curve will be concave up, with a decreased slope. This difference in shape and slope result from an added element of variability due to some items being recollected. Patients with anterograde amnesia are unable to recollect, so their Yonelinas zROC curve would have a slope close to 1.0.[6]

Area Under Curve

The Area Under Curve (AUC) is equal to the probability that a classifier will rank a randomly chosen positive instance higher than a randomly chosen negative one.[7] It can be shown that the area under the ROC curve is closely related to the Mann–Whitney U,[8][9] which tests whether positives are ranked higher than negatives. It is also equivalent to the Wilcoxon test of ranks.[9] The AUC is related to the Gini coefficient (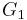G_1) by the formula 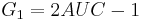G_1 = 2 AUC - 1, where:

G_1 = 1 - \sum_{k=1}^{n} (X_{k} - X_{k-1}) (Y_{k} %2B Y_{k-1})[10]

In this way, it is possible to calculate the AUC by using an average of a number of trapezoidal approximations.

The machine learning community most often uses the ROC AUC statistic for model comparison.[11] However, this practice has recently been questioned based upon new machine learning research that shows that the AUC is quite noisy as a classification measure [12] and has some other significant problems in model comparison.[13][14] A reliable and valid AUC estimate can be interpreted as the probability that the classifier will assign a higher score to a randomly chosen positive example than to a randomly chosen negative example. However, the critical research suggests frequent failures in obtaining reliable and valid AUC estimates. Thus, the practical value of the AUC measure has thus been called into question, raising the possibility that the AUC may actually introduce more uncertainty into machine learning classification accuracy comparisons than resolution.

Other measures

In engineering, the area between the ROC curve and the no-discrimination line is often preferred, due to its useful mathematical properties as a non-parametric statistic. This area is often simply known as the discrimination. In psychophysics, d' is the most commonly used measure.

The illustration at the top right of the page shows the use of ROC graphs for the discrimination between the quality of different algorithms for predicting epitopes. The graph shows that if one detects at least 60% of the epitopes in a virus protein, at least 30% of the output is falsely marked as epitopes.

Sometimes it can be more useful to look at a specific region of the ROC Curve rather than at the whole curve. It is possible to compute partial AUC.[15] For example, one could focus on the region of the curve with low false positive rate, which is often of prime interest for population screening tests.[16] Another common approach for classification problems in which P << N (common in bioinformatics applications) is to use a logarithmic scale for the x-axis.[17]

History

The ROC curve was first used during World War II for the analysis of radar signals before it was employed in signal detection theory.[18] Following the attack on Pearl Harbor in 1941, the United States army began new research to increase the prediction of correctly detected Japanese aircraft from their radar signals.

In the 1950s, ROC curves were employed in psychophysics to assess human (and occasionally non-human animal) detection of weak signals.[18] In medicine, ROC analysis has been extensively used in the evaluation of diagnostic tests.[19][20] ROC curves are also used extensively in epidemiology and medical research and are frequently mentioned in conjunction with evidence-based medicine. In radiology, ROC analysis is a common technique to evaluate new radiology techniques.[21] In the social sciences, ROC analysis is often called the ROC Accuracy Ratio, a common technique for judging the accuracy of default probability models.

ROC curves also proved useful for the evaluation of machine learning techniques. The first application of ROC in machine learning was by Spackman who demonstrated the value of ROC curves in comparing and evaluating different classification algorithms.[22]

See also

References

  1. ^ Signal detection theory and ROC analysis in psychology and diagnostics : collected papers; Swets, 1996
  2. ^ J. Fogarty, R. Baker, S. Hudson (2005). "Case studies in the use of ROC curve analysis for sensor-based estimates in human computer interaction". ACM International Conference Proceeding Series, Proceedings of Graphics Interface 2005. Waterloo, Ontario, Canada: Canadian Human-Computer Communications Society. http://portal.acm.org/citation.cfm?id=1089530. 
  3. ^ Glanzer, M.; Kim, K., Hilford, A., & Adams, J.K. (1999). "Slope of the receiver-operating characteristic in recognition memory". Journal of Experimental Psychology: Learning, Memory, and Cognition 25 (2): 500–513. 
  4. ^ Ratcliff, R.; McCoon, G., & Tindal, M. (1994). "Empirical generality of data from recognition memory ROC functions and implications for GMMs". Journal of Experimental Psychology: Learning, Memory, and Cognition 20: 763–785. 
  5. ^ Zhang, J.; Mueller, S. T. (2005). "A note on ROC analysis and non-parametric estimate of sensitivity". Psychometrika 70 (203-212). 
  6. ^ Yonelinas, A. P.; Kroll, N. E. A., Dobbins, I. G., Lazzara, M., & Knight, R. T. (1998). "Recolection and familiarity deficits in amnesia: Convergence of remember-know, process dissociation, and receiver operating characteristic data". Neuropsychology 12: 323–339. 
  7. ^ Fawcett, T. (2006). An introduction to ROC analysis. Pattern Recognition Letters, 27, 861–874.
  8. ^ Hanley, J.A. and McNeil, B.J. (1982). "The Meaning and Use of the Area under a Receiver Operating (ROC) Curvel Characteristic". Radiology 143 (1): 29--36. PMID 7063747. 
  9. ^ a b Mason, S. J.; Graham, N. E. (2002). "Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation". Quarterly Journal of the Royal Meteorological Society (128): 2145–2166. http://reia.inmet.gov.br/documentos/cursoI_INMET_IRI/Climate_Information_Course/References/Mason+Graham_2002.pdf. 
  10. ^ Hand, D.J., & Till, R.J. (2001). A simple generalization of the area under the ROC curve to multiple class classification problems. Machine Learning, 45, 171–186.
  11. ^ Hanley, JA; BJ McNeil (1983-09-01). "A method of comparing the areas under receiver operating characteristic curves derived from the same cases". Radiology 148 (3): 839–843. PMID 6878708. http://radiology.rsnajnls.org/cgi/content/abstract/148/3/839. Retrieved 2008-12-03. 
  12. ^ Hanczar, B., Hua, J., Sima, C., Weinstein, J., Bittner, M. and Dougherty, E.R. (2010). Small-sample precision of ROC-related estimates. Bioinformatics 26 (6): 822–830.
  13. ^ Lobo, J. M., Jiménez-Valverde, A. and Real, R. (2008), AUC: a misleading measure of the performance of predictive distribution models. Global Ecology and Biogeography, 17: 145–151.
  14. ^ Hand, D.J. (2009). Measuring classifier performance: A coherent alternative to the area under the ROC curve. Machine Learning, 77: 103–123.
  15. ^ McClish, Donna Katzman (1989-08-01). "Analyzing a Portion of the ROC Curve". Med Decis Making 9 (3): 190–195. doi:10.1177/0272989X8900900307. PMID 2668680. http://mdm.sagepub.com/cgi/content/abstract/9/3/190. Retrieved 2008-09-29. 
  16. ^ Dodd, Lori E.; Margaret S. Pepe (2003). "Partial AUC Estimation and Regression". Biometrics 59 (3): 614–623. doi:10.1111/1541-0420.00071. PMID 14601762. http://www.blackwell-synergy.com/doi/abs/10.1111/1541-0420.00071. Retrieved 2007-12-18. 
  17. ^ http://www.soe.ucsc.edu/~karplus/papers/better-than-chance-sep-07.pdf
  18. ^ a b D.M. Green and J.M. Swets (1966). Signal detection theory and psychophysics. New York: John Wiley and Sons Inc.. ISBN 0-471-32420-5. 
  19. ^ M.H. Zweig and G. Campbell (1993). "Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine". Clinical chemistry 39 (8): 561–577. PMID 8472349. 
  20. ^ M.S. Pepe (2003). The statistical evaluation of medical tests for classification and prediction. New York: Oxford. 
  21. ^ N.A. Obuchowski (2003). "Receiver operating characteristic curves and their use in radiology". Radiology 229 (1): 3–8. doi:10.1148/radiol.2291010898. PMID 14519861. 
  22. ^ Spackman, K. A. (1989). "Signal detection theory: Valuable tools for evaluating inductive learning". Proceedings of the Sixth International Workshop on Machine Learning. San Mateo, CA: Morgan Kaufmann. pp. 160–163. 

General references

Further reading

External links